23.4 Exercises

Factual

1. Suppose we want to find the vertex with minimal degree (fewest neighbors). Is an adjacency matrix or adjacency list better?

Problem 1

An adjacency list would be better: we can just assess the size of each list in constant time versus iterating over all $V$ vertices in each row of the adjacency matrix to count the number of neighbors.

Procedural

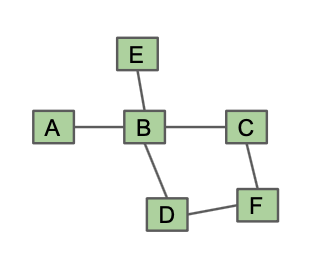
1. For the graph above, write the representation for the adjacency matrix representation.

2. Repeat (1) for the list of edges representation.

3. Repeat (1) for the adjacency list representation.

4. Run BFS starting from A for the graph above, and list the order in which vertices are visited. Break ties alphabetically.

5. Run DFS starting from A for the graph above, and list the postorder/postorder traversals. Break ties alphabetically.

Problem 1

    A  B  C  D  E  F
   
A   F  T  F  F  F  F
B   T  F  T  T  T  F
C   F  T  F  F  F  T
D   F  T  F  F  F  T
E   F  T  F  F  F  F
F   F  F  T  T  F  F

Problem 2

[{A, B}, 
{B, A}, {B, C}, {B, D}, {B, E}, 
{C, B}, {C, F},
{D, B}, {D, F},
{E, B}, 
{F, C}, {F, D}]

Problem 3

A: [B]
B: [A, C, D, E]
C: [B, F]
D: [B, F]
E: [B]
F: [C, D]

Problem 4

[A, B, C, D, E, F]

Problem 5

preorder: [A, B, C, F, D, E]

postorder: [D, F, C, E, B, A]

Metacognitive

1. Suppose we find some shortest path from a to b using BFS. Consider a vertex c that is on the path between a and b. What can we say about the shortest path from c to b?

2. Problem 4c from the Spring 2015 Midterm 2.

Problem 1

Call the original shortest path from a to b $p_{ab}$, and the path from c to b along this path $p^{*}_{cb}$. If there is some shorter path between c and b $p'_{cb}$, then we could simply take the path from a to c in the original $p_{ab}$, then take $p'_{cb}$ to find an even shorter path between a and b.

However, we stated earlier that $p_{ab}$ is the shortest path between a and b. This is a contradiction.

Thus, the shortest path between c and b must be on the shortest path between a and b.

Problem 2

Solutions are linked here and on the course website.